 |
Trax3 3.1.0
trax track library
|
 |
Trax3 3.1.0
trax track library
|
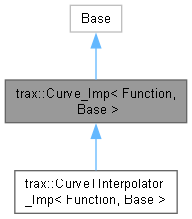
Implements a Curve that is parametrized by its arc length. More...
#include <C:/Trend/Development/Trax3/Code/trax/Curve_Imp.h>
Public Types | |
| using | DataType = typename Base::Data |
Public Member Functions | |
| Curve_Imp (Real length) noexcept | |
| bool | IsValid () const noexcept override |
| AnglePerLength | Curvature (Length s) const override |
| AnglePerLength | Torsion (Length s) const override |
| void | Transition (Length s, Position< Length > &pos) const override |
| void | Transition (Length s, Vector< One > &tan) const override |
| void | Transition (Length s, VectorBundle< Length, One > &bundle) const override |
| void | Transition (Length s, VectorBundle2< Length, One > &bundle) const override |
| void | Transition (Length s, Frame< Length, One > &frame) const override |
| std::vector< Length > | ZeroSet () const override |
| common::Interval< Length > | Range () const override |
| spat::Frame< Length, One > | GetCurveLocalTransformation () const override |
| bool | Mirror (const spat::VectorBundle< Length, One > &mirrorPlane) noexcept(noexcept(f.Mirror(mirrorPlane))) override |
| bool | Equals (const Curve &toCurve, common::Interval< Length > range, Length epsilon_length, Angle epsilon_angle) const noexcept override |
| common::Interval< Length > | Create (const DataType &data) override |
| const DataType & | GetData () const noexcept override |
Protected Member Functions | |
| Length | SampleStep () const noexcept |
| common::Interval< Length > | Sample () |
| One | t (Length s) const noexcept |
| Parameter from arc length function to evaluate f. | |
| Length | s (One t) const noexcept |
| Arc length s from parameter t calculated by bisection. | |
| bool | CheckSamples () const noexcept |
Protected Attributes | |
| Function | f |
Implements a Curve that is parametrized by its arc length.
The Function type is supposed to implement an arbitrarily parameterized curve p(t) with parameter range from 0 to 1 and its derivatives dp(t)/dt, d²p(t)/dt² and d³p(t)/dt³. There is a fictive parameter transformation t(s), which makes the function p(t(s)) be parametrized by its arc length s. It happens to be:
(1) dp/ds = dp/dt * dt/ds = D1 * dt/ds
(2) d²p/ds² = d²p/dt² * (dt/ds)² + dp/dt*d²t/ds² = D2 * (dt/ds)² + D1 * d²t/ds²
Since ds = sqrt(D1²) * dt (because (dp/ds)² = 1), we get: dt/ds = 1/sqrt(D1²) and the second derivative: d²t/ds² = -1/(2*sqrt(D1²)³) * 2 * D1*dD1/dt*dt/ds = -D1D2/(D1²D1²) from that it results:
(1) -> dp/ds = D1 / sqrt(D1²)
(2) -> d²p/ds² = (D2 - D1D2/D1² * D1) / D1²
d³p/ds³ =
For this p(t(s)) and its derivatives to s the Frenet-Formulas hold:
T = dp/ds (being a unit vector) dT/ds = kN -> k = sqrt((d²p/ds²)²) = sqrt(D2² -(D1D2)²/D1²)/D1² N = d²p/ds² / sqrt((d²p/ds²)²) B = T x N
The reparametrization of an arbitrary parametrized curve is computational demanding. So it is recommended to use this only where unavoidable.
|
inlineprotected |
p(t0+dt) = p(t0) + D1*dt + D2/2*dt² + D3/3*dt³ + ...
dS = p(t0+dt) - p(t0) = D1*dt + D2/2*dt² + ...
|dS - D1*dt| = | D2/2*dt² + ...| <= m (1)
That last equation is the positional error we'll make by our integration and we want it to stay smaller than some m. With n being the total number of integrator steps it would hold:
dL <= m * n with dL being the total error in curve length.
Since t runs from [0,1] for a fixed dt it would hold: n = 1/dt. So for that integrator step we know:
dL*dt <= m (2)
So lets assure (1) by demanding:
|dS - D1*dt| = | D2/2*dt² + ...| <= dL*dt <= m (3)
For small enough dt (<= dtMax) this could be achieved by guaranteeing:
|D2|/2*dt² <= dL*dt or: dt <= 2*dL/|D2|
|
inlineprotectednoexcept |
The default sample step might seem too coarse, especially if the progress of the curve changes fast with t. E.g. a spline assembled of cubics with different overshoots might cause problems. These can get remedied by aligning the curves lengthes with the sample step.