Space

Introduction

The spat and the dim libraries work together seemlessly to provide for our railway simulation what it calls 'the space'. A Position<Length> represents a point in this space; a Vector<One> represents a direction. Together they form a Frame<Length,One> that represents a complete frame of reference and allows for easy transformations. A velocity can be expressed as a Vector<Velocity>, an acceleration as a Vector<Acceleration>. A force might be a VectorBundle<Length,Force>, giving us both the point of application and the force vector itself.

Details

In general the trax library uses Frame<Length,One> as a frame of reference, instead of matrices. This makes it possible to work with dimensionated values:

A Frame<Length,One> representing a frame of reference in space.

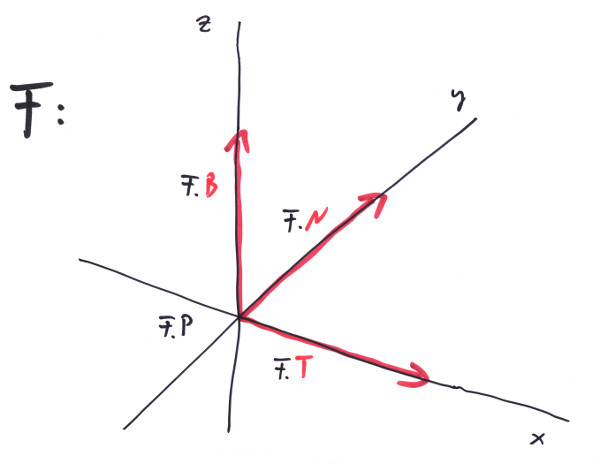
The Frame maintains a Position of dimension 'Length' and three Vectors of dimension 'One'. The three vectors are of unit length and orthogonal to each other, representing the three axes of our frame of reference. If you have a point P1, defined relative to a Frame F, it converts to global coordinates by:

Position<Length> P1 = Origin3D<Length>;     // or any other point in the Frame's local coordinates
Frame<Length,One> F = Identity<Length,One>; // or any other orthonormal Frame in global coordinates
 
Position<Length> Pglobal = F.P + P1.x * F.T + P1.y * F.N + P1.z * F.B;
 
BOOST_CHECK( Pglobal == F.ToParent( P1 ) );
BOOST_CHECK( Pglobal == F * P1  );
BOOST_CHECK( P1 == F.FromParent( Pglobal ) );

A distance vector V betweent two points in space would transform like this:

Position<Length> P2{ 1_m, 2_m, 3_m };   // pointin the Frame's local coordinates
Vector<Length> V = P2 - P1;             // distance vector in local coordinates
Vector<Length> Vglobal = V.dx * F.T + V.dy * F.N + V.dz * F.B;
 
BOOST_CHECK( Vglobal == F.ToParent( V ) );
BOOST_CHECK( Vglobal == F * V  );
BOOST_CHECK( V == F.FromParent( Vglobal ) );

Examples

Mass m = 130_kg;
Vector<Acceleration> a = G; // acceleration due to gravity
Vector<Force> F = m * a;
std::cout << "the weight of a mass of " << m << " is " << F << std::endl; // prints: "the weight of a mass of 130kg is Vector( -0kN, -0kN, -1.2753kN )"

Vector<AngularVelocity> w{ Ez<One> * 20_deg / 1_s };
Vector<Length> d{ Ex<One> * 2.8_m };
Vector<Velocity> v = w % d;
std::cout << "the momentary velocity of a point rotating around " << w << " at distance " << d << ": " << v << std::endl; // prints: "[...]  Vector( 0km/h, 3.52km/h, 0km/h )" 

To use spatial structures with dimensionated values:

Position<Length> P1{1_m,2_m,3_m};
Position<Length> P2{1_m,1_m,1_m};
 
Vector<Length> D = P2 - P1;
BOOST_CHECK( D.Length() == sqrt(5_m2) );
 
Vector<Velocity> V = D / 2_s;
BOOST_CHECK( V.Length() != 2.5_mIs );

Do also look at the tests in the test suit for further examples.